Деление чисел с фиксированной запятой в прямом и дополнительном кодах
Деление чисел с фиксированной запятой имеет ряд особенностей по сравнению с умножением. Главная из них заключается в том, что частное определяется по одному разряду за каждый цикл вычисления, а общее количество разрядов частного и, следовательно, циклов вычислений определяется, как правило, необходимой точностью, которая зависит как от точности исходных данных, так и от применяемых форматов чисел в конкретной ЭВМ.
В наиболее распространенных в настоящее время ЭВМ с системой команд X86 или IA-32 деление производится над числами с фиксированной точкой со знаком или без знака форматом байт или слово. При этом результат получается в виде целой части и остатка, причем каждая часть результата занимает фиксированное число байт.
Очевидно, что такой подход не может быть использован при делении чисел с фиксированной запятой, так как он предполагает, что, в общем случае, частное имеет целую часть, большую нуля, а это противоречит определению формата числа с фиксированной запятой. Для чисел, заданных в таком формате, будем исходить из следующих общих условий, не связанных со структурой конкретной ЭВМ:
- делимое и делитель имеют равную длину в n разрядов (для чисел, заданных в прямом коде, эти разряды предназначены лишь для хранения модуля числа);
- в случае, если делимое по абсолютной величине больше делителя, результат фиксируется как ±∞, где знак бесконечности определяется из соотношения знаков операндов;
- если делимое по абсолютной величине меньше делителя, то результат получается так же n-разрядным, как и операнды; при этом проводится вычисление n+1 разряда результата с последующим округлением до n разрядов.
Эти положения позволяют адаптировать предлагаемые алгоритмы деления к ЭВМ с произвольной архитектурой, в том числе, длине слова.
Деление чисел, заданных в прямом коде
Рассмотрим варианты деления чисел для случая, когда делимое и делитель представлены в прямом коде. При любом алгоритме деления в прямом коде чисел с фиксированной запятой результат, в общем случае, получается
При любом алгоритме деления в прямом коде чисел с фиксированной запятой результат, формируется поразрядно и так же, как и операнды, в прямом коде. Из этого следует, что в общем случае он формируется "с недостатком", так как какая-то дальнейшая цифра после прекращения выполнения операции может оказаться равной единице, тем самым увеличивая полученный результат. Это свойство может быть использовано для текущей проверки получаемых в ходе вычислений значений.
Деление со сдвигом и автоматическим восстановлением остатка
На первом этапе проводится определение знака частного:

Затем сравниваем абсолютные величины делимого и делителя.
α0 = [|X| - |Y|]дк
Если α0 ≥ 0, то |X| ≥ |Y|. Следовательно, для чисел с фиксированной запятой Z = ∞, и дальнейшее деление не имеет смысла.
Если α0 < 0, то очередные остатки при делении получаем по следующей рекуррентной формуле
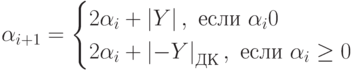 |
( 9.1) |
Очередные разряды мантиссы результата, начиная с z1, вычисляются по формуле
 |
( 9.2) |
Разряды результата получаются в прямом коде.
Здесь, как и в других рассматриваемых алгоритмах деления, при получении очередного остатка складываются числа разных знаков. Это приводит к тому, что переполнения на этом шаге деления никогда не возникает. Поэтому для выполнения данной операции модифицированный код не требуется.
Таким образом, выполнение деления согласно данному алгоритму потребует двух n-разрядных регистров для хранения модулей операндов, одного n разрядного регистра для хранения получаемых остатков, триггеров для хранения знаков операндов и результата и некоторого количества комбинационных схем для выполнения операции округления. Причем регистры модулей делимого и делителя могут быть достаточно простыми и обладать только функцией параллельной загрузки, а регистр, в котором на каждом шаге получается остаток, должен иметь также функцию сдвига в сторону старших разрядов.
Пример 9.1
Выполнить деление двух чисел с фиксированной запятой, заданных в прямом коде, по алгоритму деления со сдвигом и автоматическим восстановлением остатка: Xпк = 1.0110; Yпк = 0.1010
Решение
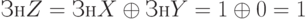
Получив достаточное количество цифр в мантиссе, запишем окончательный результат:
Пример 9.2
Выполнить деление двух чисел с фиксированной запятой, заданных в прямом коде, по алгоритму деления со сдвигом и автоматическим восстановлением остатка: Xпк = 0.1110; Yпк = 1.1010.
Решение
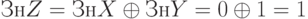
Деление со сдвигом делителя и автоматическим восстановлением остатка
Анализ формул (9.1) и (9.2) показывает, что значение очередного разряда частного зависит от соотношения удвоенного значения остатка, полученного на предыдущем шаге, и модуля делителя.
Алгоритм деления со сдвигом делителя и автоматическим восстановлением остатка базируется на определении этого же соотношения, но вместо удвоения предыдущего остатка он использует уменьшение делителя на каждом шаге в два раза. В то же время общий вид формул сохраняется:
α0 = [|X| - |Y|]дк
![\alpha_{i+1}=\begin{cases}\alpha_i+\left| Y \right|\cdot 2^{-(i+1)}, \text{ если } \alpha_i\lt0\\\alpha_i+\left[\left| -Y \right|\cdot 2^{-(i+1)},\right]_{ДК}, \text{ если } \alpha_i\geq0\end{cases}](/sites/default/files/tex_cache/5d231144b6b59e0a9d795b1289975b0e.png) |
( 9.3) |
 |
( 9.4) |
Анализируя формулу (9.3), можно сделать вывод, что схемотехнически реализация этого алгоритма потребует n-разрядного регистра для хранения модуля делимого, 2n-разрядного регистра для модуля делителя с учетом его сдвига в сторону младших разрядов, 2n-разрядного регистра для хранения остатка, комбинационные схемы для выполнения операции округления модуля частного, а также триггеры для хранения знаков операндов и результата.
Как и при выполнении операции умножения, деление без потери точности можно проводить в укороченной разрядной сетке длиной n+d разрядов, где d = log2n и, соответственно, использовать регистры меньшей разрядности. Достоинства и недостатки такого подхода рассматривались при обсуждении алгоритмов умножения в предыдущей главе. В примерах мы будем использовать 2n-разрядную сетку.
Пример 9.3
Выполнить деление двух чисел с фиксированной запятой, заданных в прямом коде, по алгоритму деления со сдвигом делителя и автоматическим восстановлением остатка: Xпк = 0.1110; Yпк = 1.1010.
Решение
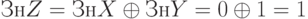
Результат:
Так как получение пятой цифры модуля частного и последующего округления мы в этом примере не рассматривали, то полученный результат соответствует тому, что было получено в примере (9.1) для тех же значений исходных данных.
Пример 9.4
Выполнить деление двух чисел с фиксированной запятой, заданных в прямом коде, по алгоритму деления со сдвигом делителя и автоматическим восстановлением остатка: Xпк = 1.0011; Yпк = 1.0110.
Решение

Получение остатка, равного нулю, при делении чисел, заданных в прямом коде, позволяет не проводить дальнейших вычислений, а записать последующие цифры результаты, равными нулю.
Таким образом, результат будет точно равен








